Here is everything you need to know about angles in a triangle including what the angles in a triangle add up to, how to find missing angles, and how to use this alongside other angle facts to form and solve equations.
There are also angles in a triangle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
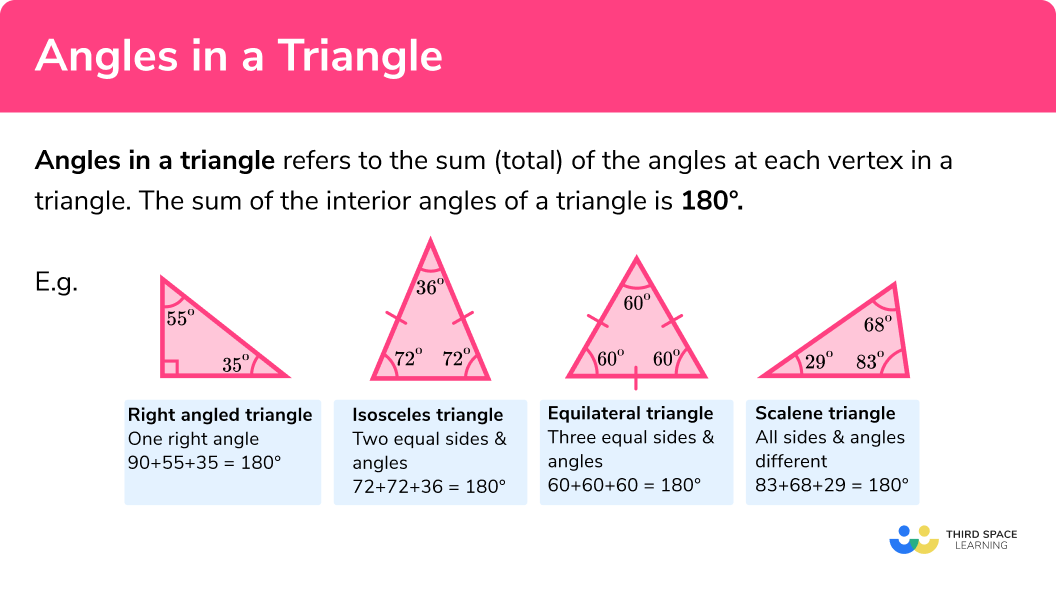
All triangles have interior angles that add up to 180º .
Angles in a triangle are the sum (total) of the angles at each vertex in a triangle.
We can use this fact to calculate missing angles by finding the total of the given angles and subtracting it from 180º .
This is true for all types of triangles.

In order to find the missing angle in a triangle:


Get your free angles in a triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions.


Get your free angles in a triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Angles in a triangle is part of our series of lessons to support revision on angles in polygons. You may find it helpful to start with the main angles in polygons lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Work out the size of the angle labelled a in the following triangle.
2 Subtract 136º from 180º .
\[180 – 136 = 44^\]Find the angle labelled b in the following triangle.
We are given the angles 90º and 19º . Add these together.
\[90 + 19 = 109^ \]Subtract 109º from 180º .
Find the angle labelled c in the following triangle.
When two sides of a triangle are equal, the angles at the ends of those sides will also be equal.
We are given the angle 64º. As this is an isosceles triangle (two equal length sides and two equal angles), the other angle at the bottom will also be 64º .
Subtract 128º from 180º .
Find the size of the angle labelled d in the triangle below.
This is an isosceles triangle. We are given one angle and asked to find one of the remaining two angles, which we know are equal.
The other two angles in this triangle add up to 70º .
Since the other two angles in this triangle are equal, we can find d by dividing by 2 .
\[70 \div 2=35^\]Sometimes the problem will involve using other angle facts.
Let’s recap some of the other angle facts we know:
These steps are interchangeable and may need to be repeated for more difficult problems.
Find the size of the angle labelled e .
Here we can use the fact that angles at a point add up to 360º .
Now we know two angles within the triangle, we can find the missing angle.
This time we already know two of the angles in the triangle so we can start by finding the third angle.
We can use the fact that opposite angles are equal to find f .
Find the size of the angle labelled g .
We know two of the angles in the right hand triangle and so we can calculate the third.
We can use the fact that angles on a straight line add up to 180º .
Since the sides of the triangle are equal, the left hand triangle is an isosceles triangle and the two angles at the bottom of the triangle are equal. Therefore we can work out the third angle.
We can use the fact that the angles in a triangle add up to 180º to form equations which we can then solve to find the values of the angles in the triangle.
Find the size of each angle in this triangle.
Add the expressions for each angle.
\[4h + 3h + 2h = 9h\]Put the simplified expression equal to 180º .
Solve the equation.
Work out the angles.
\begin 2 \times 20 = 40\\\\ 3 \times 20 = 60\\\\ 4 \times 20 = 80 \endThe three angles are 40º , 60º and 80º .
Find the size of each angle in this right-angled triangle.
Add the expressions for each angle.
\[3i + 25 + 2i – 5 + 90 = 5i + 110\]Put the simplified expression equal to 180º .
\[5i + 110 = 180\]Solve the equation.
Work out the angles.
\begin 3 \times 14+25=67\\\\ 2 \times 14-5=23 \endThe three angles are 23º , 67º and 90º .
Using 360º instead of 180º for the sum of the angles of the triangle.
Selecting the wrong angles when identifying the equal angles in an isosceles triangle (particularly a problem when the equal angles are not at the bottom). The angle that is different in an isosceles triangle is the one between the two sides with equal length.
1. Find the angle labelled z in the following triangle.




2. Find the angle labelled y .




This is an isosceles triangle and the two angles at the bottom of the triangle are equal.
3. Find the angle x in the following triangle.




This is an isosceles triangle and the two angles on the right are equal.
4. What is the size of each angle in an equilateral triangle?




All three angles in an equilateral triangle are equal so
5. Find the size of the angle labelled w in the following triangle.




The angle opposite 24^ is also 24^ since vertically opposite angles are equal.
The triangle is an isosceles triangle and the two angles on the left are the same size.
6. Find the angle labelled v .




Looking at the left hand triangle frist, we can find the missing angle in that triangle:
We can then use the fact that angles on a straight line add up to 180^ to find the unlabelled angle in the right hand triangle:
We can then find angle v :
7. Write an equation involving u and use it to find the size of each angle in the following triangle.
176^, 112^, 76^



Adding the expressions gives us:
1. Find the size of angle x given that the exterior angle shown is 153^ .
(2 marks)
Show answer(1)
(1)
2. (a) Calculate the size of angle ACE .
(b) Show that BCD is an isosceles triangle.
(5 marks)
Show answerTwo angles equal therefore isosceles
3. Work out the size of the smallest angle in the right angled triangle.
Show answer3x – 10 + 2x + 55 + 90 (= 5x + 135)
You have now learned how to:
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

© 2024 Third Space Learning. All rights reserved.
Third Space Learning is the trading name of Virtual Class Ltd
We use essential and non-essential cookies to improve the experience on our website. Please read our Cookies Policy for information on how we use cookies and how to manage or change your cookie settings.Accept
Privacy & Cookies PolicyThis website uses cookies to improve your experience while you navigate through the website. Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. We also use third-party cookies that help us analyze and understand how you use this website. These cookies will be stored in your browser only with your consent. You also have the option to opt-out of these cookies. But opting out of some of these cookies may affect your browsing experience.
Always EnabledNecessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information.
Non-necessaryAny cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website.